How to solve a Rubik's cube 4х4 - Step 6

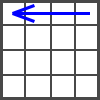
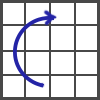
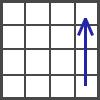
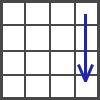
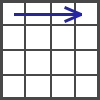
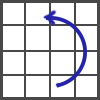
In the beginning of this stage You should have 3 solved layers. Rotate the cube how it's shown in the figure.

In the end of this step the pieces of the upper cross should be on their place. Their colors can be upturned.

Apply the formula of the fourth step for solution of 3x3 cube. You need to move the center pieces between each other till they will be in their place but it's not important how they are turned!